Nová publikace v časopise * Nature Physics * ukazuje možnost dosáhnout teoreticky optimální škálovatelnosti procesu destilace magických stavů-klíčové fáze při budování velkých kvantových počítačů odolných proti chybám. Tento průlomový vývoj řeší dlouhodobý problém v kvantovém výpočtu a otevírá cestu k efektivnějšímu provádění složitých kvantových algoritmů.
Kvantové počítače slibují revoluci v odvětvích, jako je Medicína, Věda o materiálech a umělá inteligence, pomocí jedinečných vlastností kvantové mechaniky. Tyto křehké systémy jsou však extrémně citlivé na chyby způsobené hlukem prostředí. Tento ” šum ” může rychle zničit zranitelné kvantové stavy, které jsou pro výpočet nezbytné, a zabránit tak pokroku ve směru praktického použití.
Aby vědci odolali této křehkosti, používají chybové korekční kódy — složité matematické nástroje určené k ochraně kvantových informací. Ale i pomocí korekce chyb existuje klíčové omezení: tyto kódy v podstatě podporují jednodušší kvantové operace zvané kalibrované brány. Abychom mohli provádět složitější výpočty, které nabízejí skutečné výhody oproti klasickým počítačům, potřebujeme další “nekalibrované” brány.
Zde přichází na pomoc destilace magických stavů. Tato technika, představená v roce 2005 Bravi a Kitajevem, umožňuje vytváření nekalibrovaných bran pomocí speciálně připravených kvantových stavů nazývaných magické stavy. Tyto stavy mají jedinečné vlastnosti, které nejsou dostupné standardním chybovým korekčním kódům, což umožňuje přístup k bohatší sadě kvantových operací potřebných k dosažení skutečné kvantové výhody.
** Magická složka: mimo stabilizační stavy**
Představte si všechny možné kvantové stavy jako rozsáhlou krajinu. Stabilizační stavy — království, ve kterém s ním mohou Klasické Počítače držet krok-zabírají relativně malou část této krajiny. Za touto zónou leží magické stavy, které vykazují “kvantovou kontextualitu” – další zdroj nedostupný klasickým systémům. Tyto stavy jsou klíčové pro odhalení plného potenciálu kvantových výpočtů.
Představte si magické stavy jako vzácné ingredience v receptu: umožňují vám vytvářet složitá a chutná jídla (složité kvantové výpočty), která nelze připravit pouze pomocí jednodušších ingrediencí. Počáteční verze “magických stavů” jsou však často hlučné a náchylné k chybám. Právě zde začíná destilace-čistí tyto stavy, snižuje chyby a zvyšuje jejich užitečnost.
** Hlavolam efektivity: škálování nákladů**
Klíčovou otázkou pro praktický kvantový výpočet je, jak efektivně lze destilovat magické stavy. Účinnost se měří * * náklady**: poměr hlučných vstupních stavů potřebných k výrobě jednoho vysoce kvalitního výstupního stavu. Malé náklady znamenají efektivnější využití cenných kvantových zdrojů.
V průběhu let se tyto náklady zvyšovaly,jak jsme se snažili o stále nižší víkendové chyby. Toto měřítko bylo kvantifikováno parametrem γ (gama), kde menší γ indikuje lepší účinnost. V předchozích studiích bylo dosaženo značného pokroku-až do γ ≈ 0,678 a později aproximace γ = 0 — ale praktická implementace zůstala nedosažitelná.
** Prolomení bariéry: získání trvalých nákladů**
Ve své průlomové studii Wills a jeho kolegové dosáhli stálých nákladů a prokázali, že γ může být přesně nulová pro qubitové systémy (stavební bloky kvantových počítačů). Tento čin spáchali dvěma způsoby:
-
-
- Použití kódů algebraické geometrie: * * místo dříve používaných kódů Reed-Mueller nebo Reed-Solomon se obrátili na kódy algebraické geometrie. Tyto kódy jsou známé svou výjimečnou schopností opravovat chyby při práci se systémy pevné velikosti kvantových qubitů-což je zásadně důležité pro praktické implementace.
-
-
-
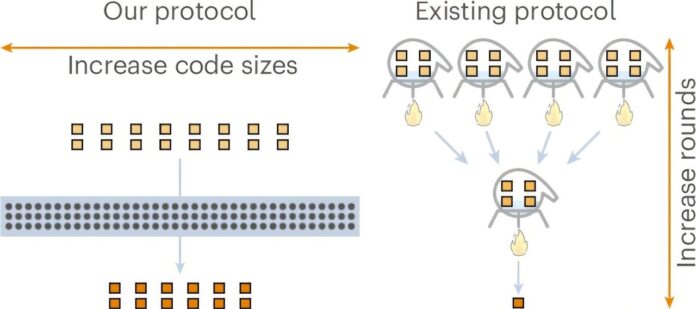
- Překlenutí mezery mezi kudity a qubity:** ačkoli jejich původní teoretický objev pracoval s kudity (kvantové systémy s 1 024 úrovněmi), Willsův tým chytře našel způsob, jak převést tento protokol konstantní zátěže do standardních qubitových systémů používaných ve skutečných experimentech. To zahrnovalo zobrazení vícerozměrných kudrlin na dostupné sady qubitů, což minimalizovalo ztrátu nákladů během konverze.
-
** Pohled vpřed: od teorie k realitě**
Tento teoretický úspěch stanovuje základní limit pro účinnost destilace magických stavů, což dokazuje, že γ = 0 je dosažitelné. Převedení tohoto do praktických implementací však představuje významné výzvy. I když je teoreticky optimální, protokol může vyžadovat více fyzikálních qubitů, než současné kvantové počítače zvládnou.
Stanovení těchto základních teoretických limitů je však kritické pro vedení budoucího výzkumu a vývoje v oblasti kvantových výpočtů odolných vůči chybám. Práce týmu otevírá nové cesty výzkumu:
-
-
- Optimalizace fixních koeficientů: * * zdokonalení dílů, aby se minimalizovaly veškeré zbývající náklady vzniklé při praktické realizaci.
-
-
-
- Výzkum kvantových kódů LDPC: * * výzkum možností kódů s nízkou hustotou testovacích matic (LDPC), známých svou spolehlivou korekcí chyb v klasickém výpočtu, pro potenciální použití v kvantové destilaci magických stavů.
-
-
-
- Identifikace optimálních transformací qubit: * * hledání ještě účinnějších způsobů, jak zobrazit kudity na qubitových systémech, další snižování nákladů a překlenutí mezery mezi teorií a praxí.
-
Cesta ke škálovatelným a odolným kvantovým počítačům je poseta jak teoretickými průlomy, tak praktickými inženýrskými problémy. Nedávné potvrzení teoreticky optimální destilace magických stavů je důležitým krokem v tomto nepřetržitém úsilí. To zdůrazňuje pokrok v porozumění a řízení kvantových systémů, který nás přibližuje k využití jejich plného potenciálu k řešení skutečných problémů.