Erreichen der theoretischen Grenze bei der Destillation von magischen Zuständen für Quantencomputer

Eine neue Studie, die in Nature Physics veröffentlicht wurde, zeigt, dass es möglich ist, theoretisch eine optimale Skalierung für die Destillation des magischen Zustands zu erreichen – ein entscheidender Prozess für den Bau großer, fehlertoleranter Quantencomputer. Dieser Durchbruch adressiert eine langjährige Herausforderung im Quantencomputing und ebnet den Weg für eine effizientere Ausführung komplexer Quantenalgorithmen.

Quantencomputer versprechen, Bereiche wie Medizin, Materialwissenschaften und künstliche Intelligenz zu revolutionieren, indem sie die einzigartigen Eigenschaften der Quantenmechanik nutzen. Diese empfindlichen Systeme sind jedoch extrem anfällig für Fehler, die durch Umgebungsgeräusche verursacht werden. Dieses “Rauschen” kann die fragilen Quantenzustände, die für die Berechnung benötigt werden, schnell zerstören und den Fortschritt in Richtung praktischer Anwendungen behindern.

Um dieser Fragilität entgegenzuwirken, setzen Forscher auf Fehlerkorrekturcodes – ausgeklügelte mathematische Werkzeuge zum Schutz von Quanteninformationen. Aber auch bei der Fehlerkorrektur gibt es eine wichtige Einschränkung: Diese Codes unterstützen hauptsächlich einfachere Quantenoperationen, die als Clifford-Gatter bekannt sind. Um komplexere Berechnungen durchzuführen, die echte Vorteile gegenüber klassischen Computern bieten, benötigen wir zusätzliche “Nicht-Clifford” -Gatter.

Hier kommt die magische Staatsdestillation ins Spiel. Diese Technik wurde 2005 von Bravyi und Kitaev eingeführt und ermöglicht die Erzeugung von Nicht-Clifford-Gattern unter Verwendung speziell präparierter Quantenzustände, die als ** magische Zustände ** bezeichnet werden. Diese Zustände besitzen einzigartige Eigenschaften, die über die hinausgehen, die Standardfehlerkorrekturcodes zugänglich sind, und ermöglichen den Zugriff auf einen reichhaltigeren Satz von Quantenoperationen, die für einen echten Quantenvorteil erforderlich sind.

** Die magische Zutat: Jenseits der Stabilisatorzustände**

Stellen Sie sich alle möglichen Quantenzustände als eine riesige Landschaft vor. Stabilisatorzustände – der Bereich, in dem klassische Computer mithalten können – nehmen in dieser Landschaft eine relativ kleine Region ein. Jenseits dieser Zone liegen magische Zustände, die “Quantenkontextualität” aufweisen – eine zusätzliche Ressource, die klassischen Systemen nicht zur Verfügung steht. Diese Zustände sind entscheidend, um das volle Potenzial der Quantenberechnung auszuschöpfen.

Stellen Sie sich magische Zustände wie seltene Zutaten in einem Rezept vor: Sie ermöglichen es Ihnen, komplexe und geschmackvolle Gerichte (komplexe Quantenberechnungen) zu kreieren, die mit einfacheren Zutaten allein nicht zubereitet werden können. Die anfänglich erzeugten “Magic State” -Versionen sind jedoch häufig verrauscht und fehleranfällig. Hier kommt die Destillation ins Spiel – sie reinigt diese Zustände, reduziert Fehler und erhöht ihren Nutzen.

** Das Effizienzrätsel: Skalierungsaufwand**

Die Schlüsselfrage für das praktische Quantencomputing ist, wie effizient die Destillation des magischen Zustands durchgeführt werden kann. Die Effizienz wird durch den ** Overhead ** gemessen: das Verhältnis der verrauschten Eingangszustände, die benötigt werden, um einen einzelnen hochwertigen Ausgangszustand zu erzeugen. Ein geringerer Overhead bedeutet eine effizientere Nutzung wertvoller Quantenressourcen.

Seit Jahren steigt dieser Overhead, da wir auf immer niedrigere Fehlerraten in den Ausgangszuständen drängen. Diese Skalierung wurde durch einen Parameter namens γ (Gamma) quantifiziert, wobei ein kleineres γ eine bessere Effizienz anzeigt. Frühere Forschungen hatten bedeutende Fortschritte gemacht – sie erreichten γ ≈ 0,678 und näherten sich später γ = 0 -, aber die praktische Umsetzung blieb schwer fassbar.

** Die Barriere durchbrechen: Konstanten Overhead erreichen**

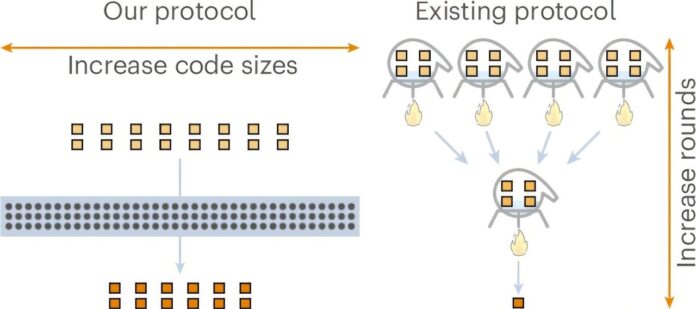
In ihrer bahnbrechenden Studie erzielten Wills und Kollegen einen konstanten Overhead, indem sie zeigten, dass γ für Qubit-Systeme (die Bausteine von Quantencomputern) genau Null sein kann. Sie haben dieses Kunststück durch einen zweigleisigen Ansatz vollbracht:

• ** Nutzung algebraischer Geometriecodes: ** Anstelle der zuvor verwendeten Reed-Muller- oder Reed-Solomon-Codes wandten sie sich algebraischen Geometriecodes zu. Diese Codes sind bekannt für ihre außergewöhnlichen Fehlerkorrekturfähigkeiten bei der Arbeit mit Quantensystemen fester Größe – unerlässlich für praktische Implementierungen.
• ** Überbrückung der Qudit-Qubit-Lücke: ** Während ihr erster theoretischer Durchbruch mit Qudits (Quantensystemen mit 1024 Stufen) funktionierte, fanden Wills und sein Team geschickt einen Weg, dieses konstante Overhead-Protokoll in Standard-Qubit-Systeme zu übersetzen, die in realen Experimenten verwendet werden. Dies beinhaltete die Abbildung der höherdimensionalen Qudits auf leicht verfügbare Sätze von Qubits, wodurch der Overhead-Verlust während der Konvertierung minimiert wurde.

Vorausschauend: Von der Theorie zur Realität

Diese theoretische Errungenschaft legt eine grundlegende Grenze für die Effizienz der Destillation im magischen Zustand fest und beweist, dass γ = 0 erreichbar ist. Dies in praktische Implementierungen umzusetzen, birgt jedoch erhebliche Herausforderungen. Obwohl das Protokoll theoretisch optimal ist, benötigt es möglicherweise mehr physikalische Qubits, als aktuelle Quantencomputer verarbeiten können.

Dennoch ist die Festlegung dieser grundlegenden theoretischen Grenzen für die zukünftige Forschung und Entwicklung im Bereich des fehlertoleranten Quantencomputings von entscheidender Bedeutung. Die Arbeit des Teams öffnet Türen zu neuen Erkundungswegen:

• ** Optimierung konstanter Faktoren: ** Verfeinerung von Details, um den verbleibenden Overhead bei der praktischen Umsetzung zu minimieren.
• ** Erforschung von Quanten-LDPC-Codes: ** Untersuchung von Varianten von LDPC-Codes (Low-Density Parity-Check), die für ihre robusten Fehlerkorrekturfähigkeiten im klassischen Computing bekannt sind, für eine mögliche Anwendung bei der Destillation von Quantenmagiezuständen.
• ** Identifizierung optimaler QuDit-Qubit-Konvertierungen: ** Suche nach noch effizienteren Möglichkeiten, Qudits auf Qubit-Systeme abzubilden, den Overhead weiter zu reduzieren und die Lücke zwischen Theorie und Praxis zu schließen.

Der Weg zu skalierbaren und fehlertoleranten Quantencomputern ist sowohl mit theoretischen Durchbrüchen als auch mit praktischen technischen Herausforderungen gepflastert. Die jüngste Demonstration der theoretisch optimalen Destillation im magischen Zustand stellt einen bedeutenden Meilenstein in dieser laufenden Suche dar. Es unterstreicht die Fortschritte beim Verständnis und der Manipulation von Quantensystemen und bringt uns der Nutzung ihres vollen Potenzials zur Lösung realer Probleme näher.