Alcanzando el Límite Teórico en la Destilación del Estado Mágico para la Computación Cuántica

Un nuevo estudio publicado en Nature Physics demuestra que es posible lograr una escala teóricamente óptima para la destilación del estado mágico, un proceso crucial para construir computadoras cuánticas grandes y tolerantes a fallas. Este avance aborda un desafío de larga data en la computación cuántica y allana el camino para una ejecución más eficiente de algoritmos cuánticos complejos.

Las computadoras cuánticas prometen revolucionar campos como la medicina, la ciencia de los materiales y la inteligencia artificial al aprovechar las propiedades únicas de la mecánica cuántica. Sin embargo, estos delicados sistemas son extremadamente susceptibles a errores causados por el ruido ambiental. Este “ruido” puede destruir rápidamente los frágiles estados cuánticos necesarios para la computación, obstaculizando el progreso hacia aplicaciones prácticas.

Para combatir esta fragilidad, los investigadores dependen de códigos de corrección de errores, sofisticadas herramientas matemáticas diseñadas para proteger la información cuántica. Pero incluso con la corrección de errores, existe una limitación clave: estos códigos admiten principalmente operaciones cuánticas más simples conocidas como puertas de Clifford. Para realizar cálculos más complejos que ofrezcan ventajas genuinas sobre las computadoras clásicas, necesitamos puertas adicionales “que no sean de Clifford”.

Aquí es donde entra en juego la destilación del estado mágico. Introducida en 2005 por Bravyi y Kitaev, esta técnica permite la creación de puertas que no son de Clifford mediante el uso de estados cuánticos especialmente preparados llamadosestados mágicos. Estos estados poseen propiedades únicas más allá de las accesibles a los códigos estándar de corrección de errores, lo que permite el acceso a un conjunto más rico de operaciones cuánticas necesarias para una verdadera ventaja cuántica.

** El Ingrediente Mágico: Más Allá de los Estados Estabilizadores**

Imagina todos los estados cuánticos posibles como un vasto paisaje. Los estados estabilizadores, el ámbito donde las computadoras clásicas pueden seguir el ritmo, ocupan una región relativamente pequeña dentro de este panorama. Más allá de esta zona se encuentran los estados mágicos, que exhiben “contextualidad cuántica”, un recurso adicional que no está disponible para los sistemas clásicos. Estos estados son cruciales para desbloquear todo el potencial de la computación cuántica.

Piense en los estados mágicos como ingredientes raros en una receta: le permiten crear platos complejos y sabrosos (cálculos cuánticos complejos) que no se pueden hacer solo con ingredientes más simples. Sin embargo, las versiones iniciales de” estado mágico ” producidas a menudo son ruidosas y propensas a errores. Aquí es donde entra la destilación: purifica estos estados, reduce los errores y aumenta su utilidad.

** El Rompecabezas de la Eficiencia: Gastos Generales de Escala**

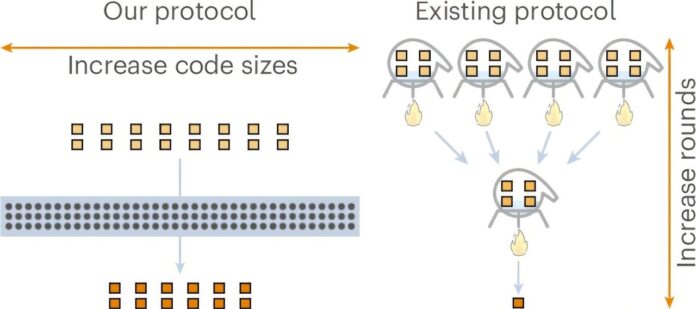
La pregunta clave para la computación cuántica práctica es qué tan eficientemente se puede realizar la destilación del estado mágico. La eficiencia se mide por la sobrecarga : la relación de estados de entrada ruidosos necesarios para producir un solo estado de salida de alta calidad. Una sobrecarga menor significa un uso más eficiente de valiosos recursos cuánticos.

Durante años, esta sobrecarga ha aumentado a medida que impulsamos tasas de error cada vez más bajas en los estados de salida. Esta escala se cuantificó mediante un parámetro llamado γ (gamma), donde un γ más pequeño indica una mejor eficiencia. Investigaciones anteriores habían logrado avances significativos, alcanzando γ ≈ 0.678 y luego acercándose a γ = 0, pero la implementación práctica seguía siendo difícil de alcanzar.

** Rompiendo la Barrera: Logrando una Sobrecarga Constante**

En su innovador estudio, Wills y sus colegas lograron una sobrecarga constante al demostrar que γ puede ser exactamente cero para los sistemas qubit (los componentes básicos de las computadoras cuánticas). Lograron esta hazaña a través de un enfoque doble:

• • • Aprovechando los códigos de Geometría Algebraica: * * En lugar de los códigos Reed-Muller o Reed-Solomon utilizados anteriormente, recurrieron a códigos de geometría algebraica. Estos códigos son conocidos por sus excepcionales capacidades de corrección de errores al trabajar con sistemas cuánticos de tamaño fijo, esenciales para implementaciones prácticas.
• • • Cerrando la brecha Qudit-Qubit: * * Si bien su avance teórico inicial funcionó con qudits( sistemas cuánticos con 1024 niveles), Wills y su equipo encontraron inteligentemente una manera de traducir este protocolo de sobrecarga constante en sistemas qubit estándar utilizados en experimentos del mundo real. Esto implicó mapear los qudits de dimensiones más altas de nuevo en conjuntos de qubits fácilmente disponibles, minimizando la pérdida de sobrecarga durante la conversión.

** Mirando hacia el futuro: De la Teoría a la Realidad**

Este logro teórico establece un límite fundamental para la eficiencia de destilación en estado mágico, demostrando que γ = 0 es alcanzable. Sin embargo, traducir esto en implementaciones prácticas presenta desafíos significativos. Aunque teóricamente es óptimo, el protocolo puede requerir más qubits físicos de los que pueden manejar las computadoras cuánticas actuales.

Sin embargo, establecer estos límites teóricos fundamentales es crucial para guiar la investigación y el desarrollo futuros en computación cuántica tolerante a fallas. El trabajo del equipo abre las puertas a nuevas vías de exploración:

• • • Optimización de factores constantes: * * Refinamiento de detalles para minimizar los gastos generales restantes incurridos durante la implementación práctica.
• • • Explorando códigos LDPC cuánticos: * * Investigando variantes de códigos de Verificación de Paridad de Baja Densidad (LDPC), conocidos por sus sólidas capacidades de corrección de errores en la computación clásica, para una posible aplicación en la destilación cuántica de estados mágicos.
• • • Identificación de conversiones óptimas de QuDit-Qubit: * * Búsqueda de formas aún más eficientes de asignar qudits a sistemas qubit, reduciendo aún más los gastos generales y cerrando la brecha entre la teoría y la práctica.

El viaje hacia computadoras cuánticas escalables y tolerantes a fallas está plagado de avances teóricos y desafíos prácticos de ingeniería. La reciente demostración de destilación de estado mágico teóricamente óptima representa un hito significativo en esta búsqueda en curso. Subraya el progreso realizado en la comprensión y manipulación de los sistemas cuánticos, acercándonos a aprovechar todo su potencial para resolver problemas del mundo real.