Atteindre la Limite Théorique de la Distillation d’État Magique pour l’Informatique Quantique

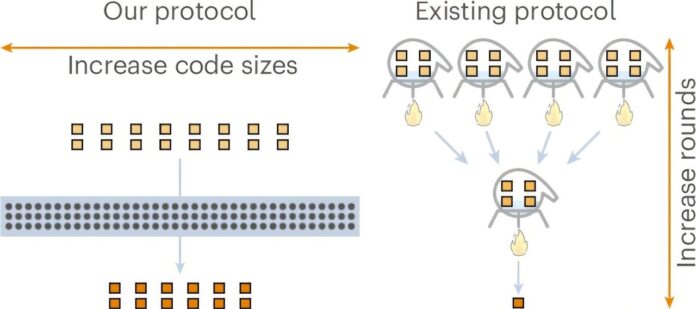
Une nouvelle étude publiée dans Nature Physics démontre qu’il est possible d’obtenir une mise à l’échelle théoriquement optimale pour la distillation de l’état magique – un processus crucial pour la construction de grands ordinateurs quantiques tolérants aux pannes. Cette percée répond à un défi de longue date de l’informatique quantique et ouvre la voie à une exécution plus efficace d’algorithmes quantiques complexes.

Les ordinateurs quantiques promettent de révolutionner des domaines tels que la médecine, la science des matériaux et l’intelligence artificielle en exploitant les propriétés uniques de la mécanique quantique. Cependant, ces systèmes délicats sont extrêmement sensibles aux erreurs causées par le bruit ambiant. Ce “bruit” peut rapidement détruire les états quantiques fragiles nécessaires au calcul, entravant les progrès vers des applications pratiques.

Pour lutter contre cette fragilité, les chercheurs s’appuient sur des codes de correction d’erreurs – des outils mathématiques sophistiqués conçus pour protéger l’information quantique. Mais même avec la correction d’erreurs, une limitation clé existe: ces codes prennent principalement en charge des opérations quantiques plus simples appelées portes de Clifford. Pour effectuer des calculs plus complexes qui offrent de réels avantages par rapport aux ordinateurs classiques, nous avons besoin de portes supplémentaires “non Clifford”.

C’est là qu’intervient la distillation à l’état magique. Introduite en 2005 par Bravyi et Kitaev, cette technique permet la création de portes non Clifford en utilisant des états quantiques spécialement préparés appelés * * états magiques**. Ces états possèdent des propriétés uniques au-delà de celles accessibles aux codes de correction d’erreurs standard, permettant d’accéder à un ensemble plus riche d’opérations quantiques nécessaires à un véritable avantage quantique.

** L’Ingrédient Magique: Au-delà des États Stabilisateurs**

Imaginez tous les états quantiques possibles comme un vaste paysage. Les États stabilisateurs – le domaine où les ordinateurs classiques peuvent suivre le rythme-occupent une région relativement petite dans ce paysage. Au – delà de cette zone se trouvent des états magiques, présentant une “contextualité quantique” – une ressource supplémentaire indisponible pour les systèmes classiques. Ces états sont cruciaux pour libérer tout le potentiel du calcul quantique.

Pensez aux états magiques comme des ingrédients rares dans une recette: ils vous permettent de créer des plats complexes et savoureux (calculs quantiques complexes) qui ne peuvent pas être préparés avec des ingrédients plus simples seuls. Cependant, les versions initiales” magic state ” produites sont souvent bruyantes et sujettes aux erreurs. C’est là qu’intervient la distillation – elle purifie ces états, réduisant les erreurs et augmentant leur utilité.

** Le Casse-Tête de l’Efficacité: Mise à l’échelle des frais généraux**

La question clé pour l’informatique quantique pratique est de savoir avec quelle efficacité la distillation d’état magique peut être effectuée. L’efficacité est mesurée par la * * surcharge**: le rapport des états d’entrée bruyants nécessaires pour produire un seul état de sortie de haute qualité. Une surcharge réduite signifie une utilisation plus efficace des précieuses ressources quantiques.

Pendant des années, cette surcharge a augmenté à mesure que nous nous efforcions d’obtenir des taux d’erreur toujours plus bas dans les états de sortie. Cette mise à l’échelle a été quantifiée par un paramètre appelé γ (gamma), où un γ plus petit indique une meilleure efficacité. Des recherches antérieures avaient fait des progrès significatifs – atteignant γ ≈ 0,678 et approchant plus tard γ = 0 – mais la mise en œuvre pratique restait insaisissable.

** Briser la barrière: Atteindre des Frais généraux constants**

Dans leur étude révolutionnaire, Wills et ses collègues ont réalisé une surcharge constante en démontrant que γ peut être exactement nul pour les systèmes qubit (les éléments constitutifs des ordinateurs quantiques). Ils ont accompli cet exploit grâce à une approche à deux volets:

• • • Tirer parti des codes de géométrie algébrique:* * Au lieu des codes Reed-Muller ou Reed-Solomon précédemment utilisés, ils se sont tournés vers les codes de géométrie algébrique. Ces codes sont connus pour leurs capacités exceptionnelles de correction d’erreurs tout en travaillant avec des systèmes quantiques de taille fixe-essentiels pour des implémentations pratiques.
• • • Combler l’écart Qudit-Qubit: * * Alors que leur percée théorique initiale fonctionnait avec les qudits (systèmes quantiques à 1024 niveaux), Wills et son équipe ont intelligemment trouvé un moyen de traduire ce protocole à surcharge constante en systèmes qubit standard utilisés dans des expériences réelles. Cela impliquait de mapper les qudits de dimension supérieure sur des ensembles de qubits facilement disponibles, minimisant les pertes de surcharge lors de la conversion.

** Regard vers l’avenir: De la Théorie à la réalité**

Cette réalisation théorique établit une limite fondamentale pour l’efficacité de la distillation à l’état magique, prouvant que γ = 0 est réalisable. Cependant, traduire cela en implémentations pratiques présente des défis importants. Bien qu’il soit théoriquement optimal, le protocole peut nécessiter plus de qubits physiques que les ordinateurs quantiques actuels ne peuvent en gérer.

Néanmoins, l’établissement de ces limites théoriques fondamentales est crucial pour orienter les futures recherches et développements en informatique quantique tolérante aux pannes. Les travaux de l’équipe ouvrent la porte à de nouvelles avenues d’exploration:

• • • Optimisation des facteurs constants: * * Affinage des détails pour minimiser les frais généraux restants encourus lors de la mise en œuvre pratique.
• • • Exploration des codes LDPC quantiques: * * Enquête sur des variantes de codes LDPC (Low-Density Parity-Check), connus pour leurs capacités robustes de correction d’erreurs en informatique classique, pour une application potentielle dans la distillation d’état magique quantique.
• • • Identification des conversions optimales QuDit-Qubit: * * Recherche de moyens encore plus efficaces de mapper les qudits aux systèmes qubit, réduisant encore les frais généraux et comblant le fossé entre la théorie et la pratique.

Le chemin vers des ordinateurs quantiques évolutifs et tolérants aux pannes est pavé à la fois de percées théoriques et de défis d’ingénierie pratiques. La récente démonstration de la distillation théoriquement optimale de l’état magique représente une étape importante dans cette quête en cours. Il souligne les progrès réalisés dans la compréhension et la manipulation des systèmes quantiques, nous rapprochant de l’exploitation de leur plein potentiel pour résoudre des problèmes du monde réel.