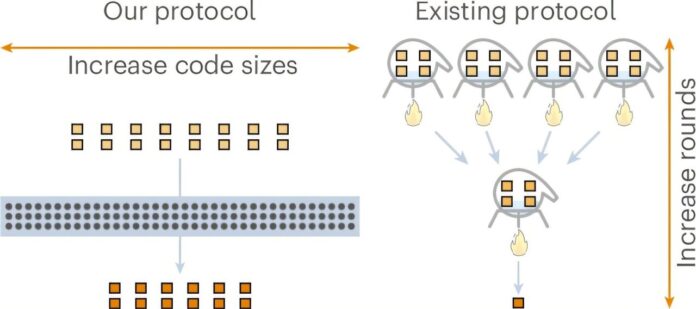
A new study published in Nature Physics demonstrates that it’s possible to achieve theoretically optimal scaling for magic state distillation – a crucial process for building large, fault-tolerant quantum computers. This breakthrough addresses a long-standing challenge in quantum computing and paves the way for more efficient execution of complex quantum algorithms.
Quantum computers promise to revolutionize fields like medicine, materials science, and artificial intelligence by harnessing the unique properties of quantum mechanics. However, these delicate systems are extremely susceptible to errors caused by environmental noise. This “noise” can quickly destroy the fragile quantum states needed for computation, hindering progress toward practical applications.
To combat this fragility, researchers rely on error correction codes – sophisticated mathematical tools designed to protect quantum information. But even with error correction, a key limitation exists: these codes primarily support simpler quantum operations known as Clifford gates. To perform more complex calculations that offer genuine advantages over classical computers, we need additional “non-Clifford” gates.
This is where magic state distillation comes in. Introduced in 2005 by Bravyi and Kitaev, this technique allows for the creation of non-Clifford gates by using specially prepared quantum states called magic states. These states possess unique properties beyond those accessible to standard error-correction codes, enabling access to a richer set of quantum operations necessary for true quantum advantage.
The Magic Ingredient: Beyond Stabilizer States
Imagine all possible quantum states as a vast landscape. Stabilizer states – the realm where classical computers can keep pace – occupy a relatively small region within this landscape. Beyond this zone lie magic states, exhibiting “quantum contextuality” – an extra resource unavailable to classical systems. These states are crucial for unlocking quantum computation’s full potential.
Think of magic states like rare ingredients in a recipe: they allow you to create complex and flavorful dishes (complex quantum computations) that cannot be made with simpler ingredients alone. However, the initial “magic state” versions produced are often noisy and prone to errors. This is where distillation comes in – it purifies these states, reducing errors and increasing their usefulness.
The Efficiency Puzzle: Scaling Overhead
The key question for practical quantum computing is how efficiently magic state distillation can be performed. Efficiency is measured by the overhead : the ratio of noisy input states needed to produce a single high-quality output state. A smaller overhead means more efficient use of precious quantum resources.
For years, this overhead has increased as we push for ever-lower error rates in output states. This scaling was quantified by a parameter called γ (gamma), where a smaller γ indicates better efficiency. Previous research had made significant strides – reaching γ ≈ 0.678 and later approaching γ = 0 – but practical implementation remained elusive.
Breaking the Barrier: Achieving Constant Overhead
In their groundbreaking study, Wills and colleagues achieved constant overhead by demonstrating that γ can be exactly zero for qubit systems (the building blocks of quantum computers). They accomplished this feat through a two-pronged approach:
- Leveraging Algebraic Geometry Codes: Instead of the previously used Reed-Muller or Reed-Solomon codes, they turned to algebraic geometry codes. These codes are known for their exceptional error correction capabilities while working with fixed-size quantum systems – essential for practical implementations.
- Bridging the Qudit-Qubit Gap: While their initial theoretical breakthrough worked with qudits (quantum systems with 1024 levels), Wills and his team cleverly found a way to translate this constant-overhead protocol into standard qubit systems used in real-world experiments. This involved mapping the higher-dimensional qudits back onto readily available sets of qubits, minimizing overhead loss during conversion.
Looking Ahead: From Theory to Reality
This theoretical achievement establishes a fundamental limit for magic state distillation efficiency, proving that γ = 0 is achievable. However, translating this into practical implementations presents significant challenges. While theoretically optimal, the protocol may require more physical qubits than current quantum computers can handle.
Nevertheless, establishing these foundational theoretical limits is crucial for guiding future research and development in fault-tolerant quantum computing. The team’s work opens doors to new avenues of exploration:
- Optimizing Constant Factors: Refining details to minimize any remaining overhead incurred during practical implementation.
- Exploring Quantum LDPC Codes: Investigating variants of Low-Density Parity-Check (LDPC) codes, known for their robust error correction capabilities in classical computing, for potential application in quantum magic state distillation.
- Identifying Optimal QuDit-Qubit Conversions: Searching for even more efficient ways to map qudits to qubit systems, further reducing overhead and bridging the gap between theory and practice.
The journey toward scalable and fault-tolerant quantum computers is paved with both theoretical breakthroughs and practical engineering challenges. The recent demonstration of theoretically optimal magic state distillation represents a significant milestone in this ongoing quest. It underscores the progress made in understanding and manipulating quantum systems, bringing us closer to harnessing their full potential for solving real-world problems.