Raggiunto il dimensionamento ottimale per la distillazione dello stato magico nell’informatica quantistica

Raggiungere il limite teorico nella distillazione dello stato magico per il calcolo quantistico

Un nuovo studio pubblicato su Nature Physics dimostra che è possibile ottenere un ridimensionamento teoricamente ottimale per la distillazione dello stato magico, un processo cruciale per la costruzione di computer quantistici di grandi dimensioni e tolleranti ai guasti. Questa svolta affronta una sfida di lunga data nel calcolo quantistico e apre la strada a un’esecuzione più efficiente di algoritmi quantistici complessi.

I computer quantistici promettono di rivoluzionare campi come la medicina, la scienza dei materiali e l’intelligenza artificiale sfruttando le proprietà uniche della meccanica quantistica. Tuttavia, questi sistemi delicati sono estremamente suscettibili agli errori causati dal rumore ambientale. Questo “rumore” può distruggere rapidamente i fragili stati quantistici necessari per il calcolo, ostacolando il progresso verso applicazioni pratiche.

Per combattere questa fragilità, i ricercatori si affidano a codici di correzione degli errori – sofisticati strumenti matematici progettati per proteggere le informazioni quantistiche. Ma anche con la correzione degli errori, esiste una limitazione chiave: questi codici supportano principalmente operazioni quantistiche più semplici note come Clifford gates. Per eseguire calcoli più complessi che offrono vantaggi reali rispetto ai computer classici, abbiamo bisogno di ulteriori porte “non Clifford”.

È qui che entra in gioco la distillazione dello stato magico. Introdotta nel 2005 da Bravyi e Kitaev, questa tecnica consente la creazione di porte non Clifford utilizzando stati quantici appositamente preparati chiamati magic states. Questi stati possiedono proprietà uniche oltre a quelle accessibili ai codici di correzione degli errori standard, consentendo l’accesso a un insieme più ricco di operazioni quantistiche necessarie per il vero vantaggio quantistico.

L’ingrediente magico: oltre gli stati stabilizzatori *

Immagina tutti i possibili stati quantici come un vasto paesaggio. Gli stati stabilizzatori – il regno in cui i computer classici possono tenere il passo-occupano una regione relativamente piccola all’interno di questo paesaggio. Al di là di questa zona si trovano stati magici, che esibiscono “contestualità quantistica” – una risorsa extra non disponibile per i sistemi classici. Questi stati sono cruciali per sbloccare il pieno potenziale della computazione quantistica.

Pensa agli stati magici come ingredienti rari in una ricetta: ti permettono di creare piatti complessi e saporiti (calcoli quantistici complessi) che non possono essere fatti con ingredienti semplici da soli. Tuttavia, le versioni iniziali dello “stato magico” prodotte sono spesso rumorose e soggette a errori. È qui che entra in gioco la distillazione: purifica questi stati, riduce gli errori e aumenta la loro utilità.

** Il puzzle dell’efficienza: Scaling Overhead**

La domanda chiave per il calcolo quantistico pratico è quanto sia efficiente la distillazione dello stato magico. L’efficienza è misurata dal * * overhead**: il rapporto tra stati di ingresso rumorosi necessari per produrre un singolo stato di uscita di alta qualità. Un sovraccarico più piccolo significa un uso più efficiente delle preziose risorse quantistiche.

Per anni, questo sovraccarico è aumentato mentre spingiamo per tassi di errore sempre più bassi negli stati di output. Questo ridimensionamento è stato quantificato da un parametro chiamato γ (gamma), dove un γ più piccolo indica una migliore efficienza. Ricerche precedenti avevano fatto passi da gigante-raggiungendo γ ≈ 0,678 e più tardi avvicinandosi γ = 0-ma l’implementazione pratica è rimasta elusiva.

** Rompere la barriera: raggiungere un sovraccarico costante**

Nel loro studio innovativo, Wills e colleghi hanno raggiunto un sovraccarico costante dimostrando che γ può essere esattamente zero per i sistemi qubit (i mattoni dei computer quantistici). Hanno compiuto questa impresa attraverso un approccio su due fronti:

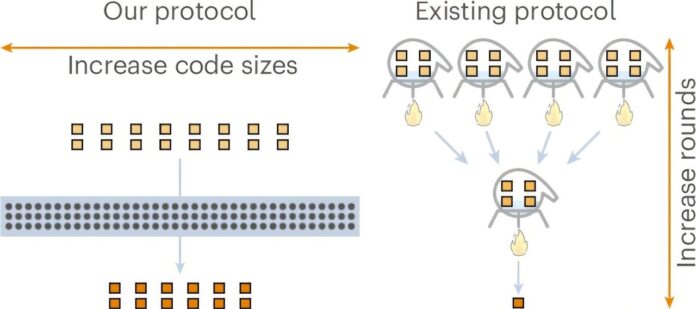
• • • Sfruttando i codici di geometria algebrica: * * Invece dei codici Reed-Muller o Reed-Solomon usati in precedenza, si sono rivolti ai codici di geometria algebrica. Questi codici sono noti per le loro eccezionali capacità di correzione degli errori mentre lavorano con sistemi quantistici di dimensioni fisse, essenziali per le implementazioni pratiche.
• • • Colmare il divario Qudit-Qubit: * * Mentre la loro svolta teorica iniziale ha funzionato con i qudit (sistemi quantistici con 1024 livelli), Wills e il suo team hanno abilmente trovato un modo per tradurre questo protocollo a sovraccarico costante in sistemi qubit standard utilizzati negli esperimenti del mondo reale. Ciò ha comportato la mappatura dei qudit di dimensione superiore su set di qubit prontamente disponibili, riducendo al minimo le perdite generali durante la conversione.

Guardare avanti: dalla teoria alla realtà *

Questo risultato teorico stabilisce un limite fondamentale per l’efficienza della distillazione dello stato magico, dimostrando che γ = 0 è realizzabile. Tuttavia, tradurre questo in implementazioni pratiche presenta sfide significative. Sebbene teoricamente ottimale, il protocollo potrebbe richiedere più qubit fisici di quelli che gli attuali computer quantistici possono gestire.

Tuttavia, stabilire questi limiti teorici fondamentali è fondamentale per guidare la ricerca e lo sviluppo futuri nel calcolo quantistico fault-tolerant. Il lavoro del team apre le porte a nuove strade di esplorazione:

• • • Ottimizzazione dei fattori costanti: * * Dettagli di raffinazione per ridurre al minimo le spese generali rimanenti sostenute durante l’implementazione pratica.
• • • Esplorare i codici quantistici LDPC: * * Studiare le varianti dei codici LDPC (Low-Density Parity-Check), noti per le loro robuste capacità di correzione degli errori nel calcolo classico, per una potenziale applicazione nella distillazione dello stato magico quantistico.
• • • Identificazione delle conversioni QuDit-Qubit ottimali: * * Ricerca di modi ancora più efficienti per mappare i qudit ai sistemi qubit, riducendo ulteriormente il sovraccarico e colmando il divario tra teoria e pratica.

Il viaggio verso computer quantistici scalabili e fault-tolerant è lastricato di scoperte teoriche e sfide ingegneristiche pratiche. La recente dimostrazione della distillazione dello stato magico teoricamente ottimale rappresenta una pietra miliare significativa in questa ricerca in corso. Sottolinea i progressi compiuti nella comprensione e nella manipolazione dei sistemi quantistici, avvicinandoci a sfruttare il loro pieno potenziale per risolvere i problemi del mondo reale.