Het bereiken van de theoretische limiet in Magic State Distillation voor Quantum Computing

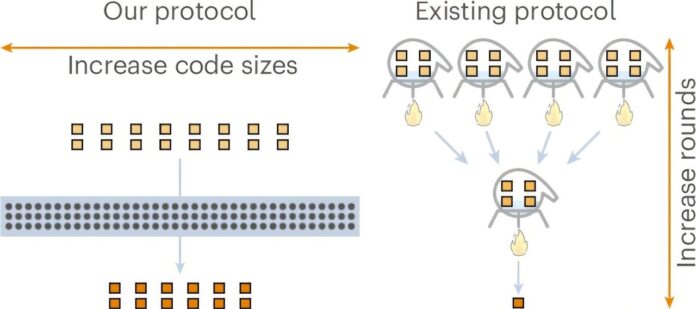
Een nieuwe studie gepubliceerd in Nature Physics toont aan dat het mogelijk is om theoretisch optimale schaalvergroting te bereiken voor Magic state distillation – een cruciaal proces voor het bouwen van grote, fouttolerante kwantumcomputers. Deze doorbraak gaat in op een al lang bestaande uitdaging in quantumcomputing en maakt de weg vrij voor een efficiëntere uitvoering van complexe quantumalgoritmen.

Kwantumcomputers beloven een revolutie teweeg te brengen in gebieden als geneeskunde, materiaalwetenschap en kunstmatige intelligentie door gebruik te maken van de unieke eigenschappen van de kwantummechanica. Deze delicate systemen zijn echter zeer gevoelig voor fouten veroorzaakt door omgevingslawaai. Deze “ruis” kan snel de fragiele kwantumtoestanden vernietigen die nodig zijn voor berekening, waardoor de vooruitgang naar praktische toepassingen wordt belemmerd.

Om deze kwetsbaarheid te bestrijden, vertrouwen onderzoekers op foutcorrectiecodes – geavanceerde wiskundige hulpmiddelen die zijn ontworpen om kwantuminformatie te beschermen. Maar zelfs met foutcorrectie bestaat er een belangrijke beperking: deze codes ondersteunen voornamelijk eenvoudiger kwantumoperaties die bekend staan als Clifford gates. Om complexere berekeningen uit te voeren die echte voordelen bieden ten opzichte van klassieke computers, hebben we extra “niet-Clifford” poorten nodig.

Dit is waar magic state distillation binnenkomt. Deze techniek werd in 2005 geïntroduceerd door Bravyi en Kitaev en maakt het mogelijk om niet-Clifford-poorten te creëren door speciaal voorbereide kwantumtoestanden te gebruiken die magische toestanden worden genoemd. Deze toestanden bezitten unieke eigenschappen die verder gaan dan die toegankelijk zijn voor standaard foutcorrectiecodes, waardoor toegang wordt verkregen tot een rijkere reeks kwantumoperaties die nodig zijn voor een echt kwantumvoordeel.

** Het Magische Ingrediënt: Beyond Stabilizer States**

Stel je alle mogelijke kwantumtoestanden voor als een uitgestrekt landschap. Stabilisatorstaten-het gebied waar klassieke computers gelijke tred kunnen houden-bezetten een relatief klein gebied binnen dit landschap. Buiten deze zone liggen magische toestanden, die “quantumcontextualiteit” vertonen – een extra bron die niet beschikbaar is voor klassieke systemen. Deze toestanden zijn cruciaal voor het ontsluiten van het volledige potentieel van kwantumcomputatie.

Denk aan magische toestanden als zeldzame ingrediënten in een Recept: ze stellen je in staat om complexe en smaakvolle gerechten te maken (complexe kwantumberekeningen) die niet alleen met eenvoudiger ingrediënten kunnen worden gemaakt. De eerste versies van de” magic state ” zijn echter vaak luidruchtig en vatbaar voor fouten. Dit is waar destillatie binnenkomt – het zuivert deze toestanden, vermindert fouten en verhoogt hun nut.

** De Efficiëntie Puzzel: Scaling Overhead**

De belangrijkste vraag voor praktische quantum computing is hoe efficiënt magic state distillation kan worden uitgevoerd. De efficiëntie wordt gemeten aan de hand van de overhead : de verhouding van lawaaierige ingangstoestanden die nodig zijn om een enkele uitgangstoestand van hoge kwaliteit te produceren. Een kleinere overhead betekent een efficiënter gebruik van kostbare kwantumbronnen.

Jarenlang is deze overhead toegenomen omdat we aandringen op steeds lagere foutenpercentages in outputtoestanden. Deze schaalvergroting werd gekwantificeerd door een parameter genaamd γ (gamma), waarbij een kleinere γ een betere efficiëntie aangeeft. Eerdere onderzoeken hadden aanzienlijke vooruitgang geboekt-het bereiken van γ ≈ 0,678 en later het naderen van γ = 0 – maar de praktische implementatie bleef ongrijpbaar.

** Het doorbreken van de barrière: het bereiken van constante Overhead**

In hun baanbrekende studie bereikten Wills en collega ‘ s constante overhead door aan te tonen dat γ precies nul kan zijn voor qubitsystemen (de bouwstenen van kwantumcomputers). Ze hebben dit bereikt door een tweeledige aanpak.:

• • • Gebruikmakend van algebraïsche meetkunde Codes: * * in plaats van de eerder gebruikte Reed-Muller of Reed-Solomon codes, wendden ze zich tot algebraïsche meetkunde codes. Deze codes staan bekend om hun uitzonderlijke foutcorrectiecapaciteiten bij het werken met kwantumsystemen van vaste grootte-essentieel voor praktische implementaties.
• • • Overbruggen van de Qudit-Qubit kloof: * * terwijl hun eerste theoretische doorbraak werkte met qudits (quantumsystemen met 1024 niveaus), vonden Wills en zijn team slim een manier om dit constant-overhead protocol te vertalen in standaard qubitsystemen die worden gebruikt in experimenten in de echte wereld. Dit omvatte het in kaart brengen van de hoger dimensionale qudits terug op gemakkelijk beschikbare sets van qubits, waardoor het overheadverlies tijdens de conversie werd geminimaliseerd.

** Vooruitkijken: van theorie naar realiteit**

Deze theoretische prestatie stelt een fundamentele grens voor de destillatie-efficiëntie in magische toestand vast, waaruit blijkt dat γ = 0 haalbaar is. Het vertalen hiervan naar praktische implementaties brengt echter grote uitdagingen met zich mee. Hoewel theoretisch optimaal, kan het protocol meer fysieke qubits vereisen dan huidige kwantumcomputers kunnen aan.

Niettemin is het vaststellen van deze fundamentele theoretische grenzen cruciaal voor het begeleiden van toekomstig onderzoek en ontwikkeling in fouttolerante kwantumcomputing. Het werk van het team opent deuren naar nieuwe wegen van verkenning:

• • • Constante factoren optimaliseren: * * details verfijnen om eventuele resterende overhead tijdens de praktische implementatie te minimaliseren.
• • • Onderzoeken van Quantum LDPC Codes: * * onderzoeken van varianten van Low-Density Parity-Check (LDPC) codes, bekend om hun robuuste foutcorrectie mogelijkheden in klassieke computing, voor mogelijke toepassing in quantum magic state distillation.
• • • Optimale Qudit-Qubit-conversies identificeren: * * zoeken naar nog efficiëntere manieren om qudits in kaart te brengen met qubit-systemen, waardoor de overhead verder wordt verminderd en de kloof tussen theorie en praktijk wordt overbrugd.

De reis naar schaalbare en fouttolerante kwantumcomputers is geplaveid met zowel theoretische doorbraken als praktische technische uitdagingen. De recente demonstratie van theoretisch optimale Magic state distillatie is een belangrijke mijlpaal in deze voortdurende zoektocht. Het onderstreept de vooruitgang die is geboekt bij het begrijpen en manipuleren van kwantumsystemen, waardoor we dichter bij het benutten van hun volledige potentieel voor het oplossen van echte problemen komen.