Osiągnięcie teoretycznego limitu w procesie destylacji Stanów magicznych do obliczeń kwantowych

Nowa publikacja w czasopiśmie * Nature Physics * pokazuje możliwość osiągnięcia teoretycznie optymalnej skalowalności procesu destylacji Stanów magicznych-kluczowego etapu w budowie dużych, odpornych na uszkodzenia komputerów kwantowych. Ten przełomowy rozwój rozwiązuje długotrwały problem w dziedzinie obliczeń kwantowych i toruje drogę do bardziej wydajnego wykonywania złożonych algorytmów kwantowych.

Komputery kwantowe obiecują zrewolucjonizować branże, takie jak medycyna, materiałoznawstwo i sztuczna inteligencja, wykorzystując unikalne właściwości mechaniki kwantowej. Jednak te delikatne systemy są niezwykle wrażliwe na błędy spowodowane hałasem otoczenia. Ten “hałas” może szybko zniszczyć bardzo potrzebne obliczeniowo wrażliwe stany kwantowe, utrudniając postęp w kierunku praktycznych zastosowań.

Aby przeciwdziałać tej kruchości, naukowcy używają kodów korekcji błędów-wyrafinowanych narzędzi matematycznych zaprojektowanych w celu ochrony informacji kwantowych. Ale nawet przy użyciu korekcji błędów istnieje kluczowe ograniczenie: kody te zasadniczo obsługują prostsze operacje kwantowe zwane skalibrowanymi bramkami. Aby wykonać bardziej złożone obliczenia, które oferują prawdziwą przewagę nad klasycznymi komputerami, potrzebujemy dodatkowej” nieskalibrowanej ” bramy.

W tym miejscu pojawia się destylacja Stanów magicznych. Wprowadzona w 2005 roku przez Braviego i Kitaeva technika ta umożliwia tworzenie nieskalibrowanych bram za pomocą specjalnie przygotowanych stanów kwantowych zwanych Stanami magicznymi. Stany te mają unikalne właściwości niedostępne dla standardowych kodów korekcji błędów, co zapewnia dostęp do bogatszego zestawu operacji kwantowych potrzebnych do osiągnięcia prawdziwej przewagi kwantowej.

** Magiczny składnik: poza Stanami stabilizującymi**

Wyobraź sobie wszystkie możliwe Stany kwantowe jako rozległy krajobraz. Stany stabilizacyjne — królestwo, w którym Klasyczne komputery mogą nadążyć-zajmują stosunkowo niewielki obszar tego krajobrazu. Za tą strefą leżą Stany magiczne, które wykazują “kwantową kontekstualność” – dodatkowy zasób niedostępny dla klasycznych systemów. Stany te są kluczowe dla odblokowania pełnego potencjału obliczeń kwantowych.

Wyobraź sobie magiczne Stany jako rzadkie składniki w przepisie: pozwalają tworzyć złożone i smaczne posiłki (złożone obliczenia kwantowe), których nie można przygotować przy użyciu tylko prostszych składników. Jednak początkowe wersje “Stanów magicznych” są często hałaśliwe i podatne na błędy. W tym miejscu rozpoczyna się destylacja — oczyszcza te stany, zmniejszając błędy i zwiększając ich użyteczność.

** Zagadka efektywności: skalowanie kosztów**

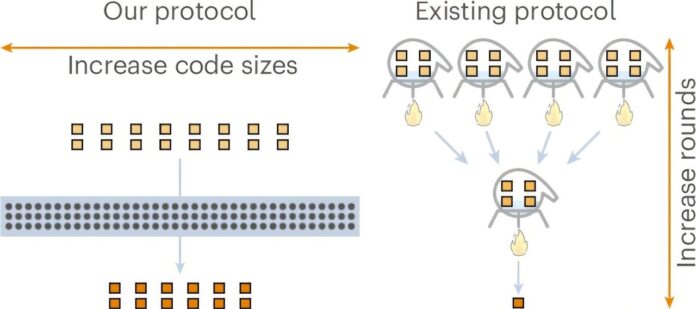
Kluczową kwestią dla praktycznych obliczeń kwantowych jest to, jak skutecznie można przeprowadzić destylację Stanów magicznych. Wydajność jest mierzona * * kosztem**: stosunek hałaśliwych Stanów wejściowych wymaganych do wytworzenia jednego wysokiej jakości stanu wyjściowego. Małe koszty oznaczają bardziej efektywne wykorzystanie cennych zasobów kwantowych.

Przez lata koszty te rosły, gdy dążyliśmy do coraz niższych błędów stanu wyjściowego. To skalowanie zostało określone ilościowo za pomocą parametru γ (gamma), gdzie mniejsze γ wskazuje na lepszą wydajność. W poprzednich badaniach poczyniono znaczne postępy-do γ ≈ 0,678 i późne przybliżenie γ = 0-ale praktyczna realizacja pozostała nieosiągalna.

** Przełamanie bariery: uzyskanie kosztów stałych**

W swoich przełomowych badaniach Wills i jego koledzy osiągnęli koszty stałe, udowadniając, że γ może być dokładnie zerowe dla Systemów kubitów (elementów składowych komputerów kwantowych). Dokonali tego wyczynu na dwa sposoby:

• • • Korzystanie z kodów geometrii algebraicznej: * * zamiast wcześniej używanych kodów Reed-Mueller lub Reed-Solomon, zwrócili się do kodów geometrii algebraicznej. Kody te są znane ze swojej wyjątkowej zdolności do korygowania błędów podczas pracy z systemami o stałej wielkości kubitów kwantowych-co ma zasadnicze znaczenie dla praktycznych implementacji.
• • • Wypełnianie luki między kuditami i kubitami: * * chociaż ich początkowe odkrycie teoretyczne działało z kuditami (układami kwantowymi o 1024 poziomach), zespół Willsa sprytnie znalazł sposób na przetłumaczenie tego protokołu stałego obciążenia na standardowe systemy kubitów używane w rzeczywistych eksperymentach. Obejmowało to mapowanie wielowymiarowych kuditów na dostępne zestawy kubitów, minimalizując stratę kosztów podczas transformacji.

** Spojrzenie w przyszłość: od teorii do rzeczywistości**

To osiągnięcie teoretyczne wyznacza podstawową granicę wydajności destylacji Stanów magicznych, udowadniając, że γ = 0 jest osiągalne. Przełożenie tego na praktyczne wdrożenia stwarza jednak znaczące wyzwania. Chociaż teoretycznie optymalny, protokół może wymagać więcej fizycznych kubitów niż nowoczesne komputery kwantowe mogą obsłużyć.

Jednak ustalenie tych podstawowych granic teoretycznych ma kluczowe znaczenie dla kierowania przyszłymi badaniami i rozwojem w dziedzinie odpornych na uszkodzenia obliczeń kwantowych. Praca zespołu otwiera nowe drogi badawcze:

• • • Optymalizacja stałych współczynników: * * Udoskonalenie części w celu zminimalizowania wszelkich pozostałych kosztów wynikających z praktycznego wdrożenia.
• • • Badanie kodów kwantowych LDPC: * * badanie wariantów kodów o niskiej gęstości macierzy walidacyjnej (LDPC), znanych z solidnej korekcji błędów w obliczeniach klasycznych, do potencjalnych zastosowań w kwantowej destylacji Stanów magicznych.
• • • Identyfikacja optymalnych transformacji kudit-Kubit: * * znalezienie jeszcze bardziej wydajnych sposobów mapowania kuditów na systemy kubitów, dalsze zmniejszanie kosztów i wypełnianie luki między teorią a praktyką.

Droga do skalowalnych i odpornych na uszkodzenia komputerów kwantowych jest usiana zarówno przełomami teoretycznymi, jak i praktycznymi problemami inżynieryjnymi. Niedawne potwierdzenie teoretycznie optymalnej destylacji Stanów magicznych jest ważnym krokiem w tym ciągłym dążeniu. Podkreśla to poczynione postępy w zrozumieniu i zarządzaniu systemami kwantowymi, przybliżając nas do wykorzystania ich pełnego potencjału do rozwiązywania rzeczywistych problemów.