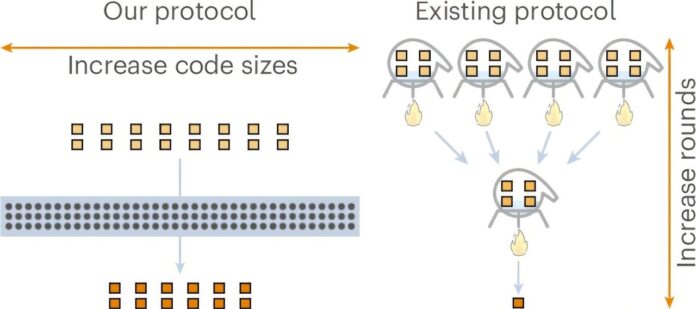
Новая публикация в журнале Nature Physics демонстрирует возможность достижения теоретически оптимальной масштабируемости процесса перегонки магических состояний — ключевого этапа в построении крупных отказоустойчивых квантовых компьютеров. Это прорывная разработка решает давнюю проблему в области квантового вычисления и открывает путь для более эффективного выполнения сложных квантовых алгоритмов.
Квантовые компьютеры обещают революционизировать такие отрасли, как медицина, материаловедение и искусственный интеллект, используя уникальные свойства квантовой механики. Однако эти хрупкие системы чрезвычайно чувствительны к ошибкам, вызванным шумом окружающей среды. Этот «шум» может быстро разрушить столь необходимые для вычислений уязвимые квантовые состояния, препятствуя прогрессу в направлении практического применения.
Чтобы противостоять этой хрупкости, исследователи используют коды коррекции ошибок — сложные математические инструменты, предназначенные для защиты квантовой информации. Но даже с использованием коррекции ошибок существует ключевое ограничение: эти коды в основном поддерживают более простые квантовые операции, называемые калиброванными воротами. Для выполнения более сложных вычислений, которые предлагают настоящие преимущества перед классическими компьютерами, нам необходимы дополнительные «некалиброванные» ворота.
Вот где приходит на помощь перегонка магических состояний. Введенная в 2005 году Брави и Китаевым, эта техника позволяет создавать некалиброванные ворота с помощью специально подготовленных квантовых состояний, называемых магическими состояниями. Эти состояния обладают уникальными свойствами, недоступными стандартным кодам коррекции ошибок, что обеспечивает доступ к более богатому набору квантовых операций, необходимых для достижения истинного квантового преимущества.
Магический ингредиент: за пределами стабилизаторных состояний
Представьте себе все возможные квантовые состояния как обширный ландшафт. Стабилизаторные состояния — царство, в котором классические компьютеры могут идти в ногу с ним — занимают относительно небольшой участок этого ландшафта. За этой зоной лежат магические состояния, проявляющие «квантовое контекстуальность» — дополнительный ресурс, недоступный классическим системам. Эти состояния являются ключевыми для раскрытия полного потенциала квантовых вычислений.
Представьте магические состояния как редкие ингредиенты в рецепте: они позволяют создавать сложные и вкусные блюда (сложные квантовые вычисления), которые невозможно приготовить с использованием только более простых ингредиентов. Однако начальные версии «магических состояний» часто шумные и подвержены ошибкам. Именно здесь начинается перегонка — она очищает эти состояния, уменьшая ошибки и повышая их полезность.
Головоломка эффективности: масштабирование издержек
Ключевым вопросом для практического квантового вычисления является то, насколько эффективно может осуществляться перегонка магических состояний. Эффективность измеряется издержками : отношение шумящих входных состояний, необходимых для производства одного высококачественного выходного состояния. Маленькие издержки означают более эффективное использование ценных квантовых ресурсов.
В течение многих лет эти издержки увеличивались по мере того, как мы стремились к все более низким ошибкам выходных состояний. Это масштабирование было количественно определено параметром γ (гамма), где меньшее γ указывает на лучшую эффективность. В предыдущих исследованиях были достигнуты значительные успехи — до γ ≈ 0,678 и позднее приближение к γ = 0 — но практическая реализация оставалась недостижимой.
Прорыв барьера: получение постоянных издержек
В своем прорывном исследовании Виллс и его коллеги достигли постоянных издержек, доказав, что γ может быть точно равна нулю для систем кубитов (строительных блоков квантовых компьютеров). Они совершили этот подвиг двумя путями:
- Использование кодов алгебраической геометрии: Вместо ранее использовавшихся кодов Рид-Мюллера или Рид-Соломона они обратились к кодам алгебраической геометрии. Эти коды известны своей исключительной способностью исправлять ошибки при работе с системами фиксированного размера квантовых кубитов — что принципиально важно для практических реализаций.
- Преодоление разрыва между кудитами и кубитами: Хотя их первоначальное теоретическое открытие работало с кудитами (квантовыми системами с 1024 уровнями), команда Виллса хитроумно нашла способ перевести этот протокол постоянной нагрузки в стандартные системы кубитов, используемые в реальных экспериментах. Это включало отображение многомерных кудитов на доступные наборы кубитов, минимизируя потерю издержек во время преобразования.
Взгляд вперед: от теории к действительности
Это теоретическое достижение устанавливает фундаментальный предел для эффективности перегонки магических состояний, доказывающий, что γ = 0 достижимо. Однако перевод этого в практические реализации ставит перед собой значительные вызовы. Хотя теоретически оптимально, протокол может требовать больше физических кубитов, чем современные квантовые компьютеры могут обрабатывать.
Тем не менее, установление этих фундаментальных теоретических пределов является критически важным для руководства будущими исследованиями и разработками в области отказоустойчивых квантовых вычислений. Работа команды открывает новые пути исследований:
- Оптимизация постоянных коэффициентов: Усовершенствование деталей для минимизации любых оставшихся издержек, возникающих при практической реализации.
- Исследование квантовых кодов LDPC: Исследование вариантов кодов с низкой плотностью проверочных матриц (LDPC), известных своей надежной коррекцией ошибок в классическом вычислении, для потенциального применения в квантовой перегонке магических состояний.
- Выявление оптимальных преобразований кудит-кубит: Поиск еще более эффективных способов отображения кудитов на системы кубитов, дальнейшее сокращение издержек и преодоление разрыва между теорией и практикой.
Путь к масштабируемым и отказоустойчивым квантовым компьютерам усеян как теоретическими прорывами, так и практическими инженерными проблемами. Недавнее подтверждение теоретически оптимальной перегонки магических состояний является важным этапом в этом непрерывном стремлении. Это подчеркивает сделанный прогресс в понимании и управлении квантовыми системами, приближая нас к использованию их полного потенциала для решения реальных задач.